モデルビュー変換
カメラとモデル
さて、いよいよ3次元プログラミングの醍醐味である変換作業に入りましょう
オブジェクトを立体空間でブイブイ言わせずして、3次元は語れません
変換処理を学ぶためには、頂点情報がどのような手順を踏んで
実際の2次元グラフィックスで描画されるかを知らなければなりません
大まかに、変換処理は次のような流れになっています
頂点情報 → モデルビュー変換 → 射影変換 → ビューポート変換 → 描画
今回は、このうちのモデルビュー変換について詳しく解説します
モデルビュー変換は、変換作業の中でも特に重要なポイントです
モデルビュー変換は視界変換とモデリング変換からなります
視界変換とは、オブジェクトを見つめるカメラであり、ユーザーの視点です
モデリング変換は、カメラが見ている被写体の位置や方向を変換する作業を言います
しかし、これらの作業はモデルビューとして一括されますが、なぜでしょうか
理由は簡単で、知世ちゃんがビデオカメラでさくらちゃんを撮影している時
さくらちゃん(モデル)がカメラに近づいても、知世ちゃん(視点)がさくらちゃんに近づいても
カメラに映し出されている映像は同じ結果を得ることになります(背景は考えないとする)
つまりは、モデルが動いてもカメラが動いても、映し出される映像は変化します
そのため、これらの変換作業はモデルビューとして一括して考えた方が理解が容易です
この時、3次元の情報を2次元に変換することをジオメトリ変換と呼びます
ジオメトリとは「幾何学」のことで、場合によってはハードウェアレベルで変換を行います
とくに、並行移動、拡大縮小、回転の図形変換をアフィン変換と呼びます
これらは3次元グラフィックスの基本用語なので覚えておいてください
変換処理には 4 × 4 の行列が用いられます
C 言語では float 型の 16 個の要素を持つ配列と考えてよいでしょう
なぜジオメトリ変換に行列を使うのかという疑問が発生すると思いますが
行列を乗算することによって、複数の移動、回転といった要素を
組み合わせて変換できるという利点があるからです
| a1 | a4 | a8 | a12 |
| a2 | a5 | a9 | a13 |
| a3 | a6 | a10 | a14 |
| a4 | a7 | a11 | a15 |
これが座標変換に用いられる 4 × 4 の行列です
C 言語の多次元配列で考えた場合、直観的な操作とは異なるので注意してください
C 言語の配列だと2番目の要素に a4 が入ります
そのため、単純に 16 この配列として固定した方が考えやすいのです
OpenGL では、自分で行列を演算して設定することも可能ですが
通常は、専用のコマンドを利用することで効率化を図ることができます
一般的には、コマンドを用いるべきだと考えられています
行列演算に関係するコマンドを利用するには、まず、次のターゲットを指定する必要があります
次の行列演算ターゲットを選択するには glMatrixMode() 関数を使います
void glMatrixMode(GLenum mode);
mode には、次の行列演算のターゲットとなる行列のスタックを指定します
ここには、次の値のいずれかを指定します
| 定数 | ターゲット |
|---|
| GL_MODELVIEW | モデルビュー行列 |
| GL_PROJECTION | 射影行列 |
| GL_TEXTURE | テクスチャ行列 |
デフォルトでは GL_MODELVIEW が設定されています
射影行列やテクスチャ行列については、この場では触れません
現在の行列を調べるには GL_MATRIX_MODE 定数を使って glGet() から得ることができます
glMatrixMode() で選択した行列が、今後のコマンドの操作対象となります
現在の行列を、任意の行列に置き換えるには glLoadMatrix() を使います
void glLoadMatrixd(const GLdouble *m);
void glLoadMatrixf(const GLfloat *m);
m には 16 個の要素を持つ配列(すなわち 4 × 4 行列)へのポインタを指定します
現在の行列は、この値に置き換えられます
事実上、この関数さえ知っていればあらゆる変換処理を実現することができますが
その場合は、行列の乗算や変換式を開発者が記述する必要があります
そこで、行列を乗算する glMultMatrix() 関数を使うことができます
void glMultMatrixd(const GLdouble *m);
void glMultMatrixf(const GLfloat *m);
m には、現在の行列に乗算する 16 個の要素を持つ配列へのポインタを指定します
この関数を使えば、乗算処理を OpenGL に委ねることができます
現在の行列を単位行列にするには glLoadIdentity() 関数を使います
単位行列とは、次の行列を glLoadMatrix() に指定するのと同じことです
これを用いることで、変換処理の累積を消去することができます
void glLoadIdentity(void);
あとは、アフィン変換を行うための方法さえわかれば
対象の行列と乗算することで、立体的な変換を行うことも可能となるでしょう
手動で変換を行う場合、例えば平行移動だと次のような行列と乗算します
x、y、z には、それぞれ平行移動する値を指定します
回転処理も行列を用いることで実現することができます
回転は少しややこしいのですが、X、Y、Z を軸に次の3つに分かれます
| 1 | 0 | 0 | 0 |
| 0 | cos θ | -sin θ | 0 |
| 0 | sin θ | cos θ | 0 |
| 0 | 0 | 0 | 1 |
| cos θ | 0 | sin θ | 0 |
| 0 | 1 | 0 | 0 |
| -sin θ | 0 | cos θ | 0 |
| 0 | 0 | 0 | 1 |
| cos θ | -sin θ | 0 | 0 |
| sin θ | cos θ | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
上から順に X 軸、Y 軸、Z 軸の周りで回転させる変換行列です
定数 θ には、回転する角度を指定します
スケーリングは次のような行列を使います
これを用いれば、頂点を拡大縮小することができます
x、y、z のそれぞれの定数は、拡大縮小のスケール係数です
1 以上であればオブジェクトが拡大され、1 より小さければ縮小されるでしょう
また、-1 にすれば線対称変換されます(つまり、反転する)
#include <math.h>
#include <windows.h>
#include <GL/gl.h>
#include <GL/glut.h>
#define ANGLE 0.2
GLfloat translate[] = {
1 , 0 , 0 , 0 ,
0 , 1 , 0 , 0 ,
0 , 0 , 1 , 0 ,
0 , 0 , 0 , 1
};
void disp( void ) {
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_POLYGON);
glColor3f(1 , 0 , 0);
glVertex2f(-0.9 , -0.9);
glColor3f(0 , 1 , 0);
glVertex2f(0 , 0.9);
glColor3f(0 , 0 , 1);
glVertex2f(0.9 , -0.9);
glEnd();
glFlush();
}
void timer(int value) {
glMultMatrixf(translate);
glutPostRedisplay();
glutTimerFunc(50 , timer , 0);
}
int main(int argc , char ** argv) {
glutInit(&argc , argv);
glutInitWindowPosition(100 , 50);
glutInitWindowSize(400 , 300);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutCreateWindow("Kitty on your lap");
glutDisplayFunc(disp);
glutTimerFunc(100 , timer , 0);
translate[0] = cos(ANGLE);
translate[2] = -sin(ANGLE);
translate[8] = sin(ANGLE);
translate[10] = cos(ANGLE);
glutMainLoop();
return 0;
}
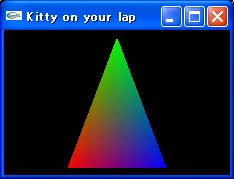
このプログラムは、手動で回転処理を行うための行列を作成し
タイマ コールバック関数で glMultMatrix() を使って乗算させています
これによって、色つきの三角形が Y 軸でクルクルと回転します
回転度数は、一回につき 0.2 を設定していますが
マクロ ANGLE を変更することによって回転速度を変更することができます
さて、ここまではかなり数学的な話になりましたが、理解することができたでしょうか?
行列を乗算すれば、平行移動や回転などを併用することも可能です
しかし、変換処理のために、わざわざ行列を用意するのは面倒ですね
そして、誰もがアフィン変換のための関数を作ろうと考えることになるでしょう
ご安心ください。すでに専用のコマンドが OpenGL によって提供されています
平行移動を行うには glTranslate() 関数を使います
void glTranslated(GLdouble x , GLdouble y , GLdouble z);
void glTranslatef(GLfloat x , GLfloat y , GLfloat z);
x、y、z には、それぞれオブジェクトを平行移動する値を指定します
例えば x に 1 を指定した場合、オブジェクトは X 座標に 1 平行移動します
回転は glRotate() を使います
void glRotated(
GLdouble angle ,
GLdouble x , GLdouble y , GLdouble z
);
void glRotatef(
GLfloat angle ,
GLfloat x , GLfloat y , GLfloat z
);
angle には回転度数を指定します
x、y、z は、回転する方向を指定するためのベクトルです
原点からこの点を通過する線を中心に、左回りでオブジェクトが回転します
内部では、次のような行列演算を行っています
このとき、c=cos(angle)、s=sin(angle) とします
| xx(1-c)+c | xy(1-c)-zs | xz(1-c)+ys | 0 |
| yx(1-c)-zs | yy(1-c)+c | yz(1-c)-xs | 0 |
| xz(1-c)-ys | yz(1-c)+xs | zz(1-c)+c | 0 |
| 0 | 0 | 0 | 1 |
スケーリングは glScaled() を使います
void glScaled(GLdouble x , GLdouble y , GLdouble z);
void glScalef(GLfloat x , GLfloat y , GLfloat z);
x、y、z には、それぞれスケーリング係数を指定します
1 以上であればオブジェクトが拡大され、1 より小さければ縮小されます
また、-1 にすれば線対称変換されます
これらの関数を使えば、わざわざ行列を作成しなくても
現在の行列に対してアフィン変換を適用することができます
#include <windows.h>
#include <GL/gl.h>
#include <GL/glut.h>
void disp( void ) {
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_POLYGON);
glColor3f(1 , 0 , 0);
glVertex2f(-0.9 , -0.9);
glColor3f(0 , 1 , 0);
glVertex2f(0 , 0.9);
glColor3f(0 , 0 , 1);
glVertex2f(0.9 , -0.9);
glEnd();
glFlush();
}
void timer(int value) {
glRotatef(2 , 0.5 , 1 , 0.25);
glutPostRedisplay();
glutTimerFunc(50 , timer , 0);
}
int main(int argc , char ** argv) {
glutInit(&argc , argv);
glutInitWindowPosition(100 , 50);
glutInitWindowSize(400 , 300);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutCreateWindow("Kitty on your lap");
glutDisplayFunc(disp);
glutTimerFunc(100 , timer , 0);
glutMainLoop();
return 0;
}
このプログラムは、glRotate() 関数を使ってモデルビュー変換を行っています
三角形が、X 軸、Y 軸、Z 軸に、複雑に回転することを確認できます
